Methodik
Ziel des Projektes ist neben einer bundesweiten Darstellung der historischen und aktuellen Grundwasserstände die monatlich aktualisierte Berechnung und Bereitstellung von kurzfristigen Grundwasserstandsvorhersagen (bis 3 Monate), mittelfristigen Grundwasserstandsprognosen (bis 10 Jahre) sowie von langfristigen Grundwasserstandsprojektionen (bis 2100) für flächendeckend über Deutschland verteilte Messstellen. Dazu wurden in einem ersten Schritt aus den umfangreichen Messstellendaten der zuständigen Landesämter mit einer bundesweit einheitlichen Methodik auf der Basis von künstlichen neuronalen Netzen (KNN) repräsentative Messstellen in sogenannten Clusterregionen ausgewählt. In einem zweiten Schritt wurden an diesen Referenzmessstellen mit einer ebenfalls KNN-basierten Methodik Grundwasserstandsvorhersagen auf der Basis von beobachteten und modellierten Klimarasterdaten des Deutschen Wetterdienstes (DWD) berechnet.
Auswahl von Referenzmessstellen:
Um aus dem von den Ländern zur Verfügung gestellten Messstellenpool die Messstellen auszuwählen, die als Referenzmessstellen und damit für die Vorhersage verwendet werden können, wurde ein neues Verfahren entwickelt, das auf einem speziellen Typ künstlich neuronaler Netze, den sogenannten selbstorganisierenden Karten (Self-Organizing Maps - SOM), basiert und einem klassischen Clusteransatz ähnelt. Ziel ist es, Gruppen von ähnlichen Objekten, in diesem Fall Grundwasserganglinien mit ähnlicher Dynamik, zu finden. Um das Problem ungleicher Zeitreihenlängen und Datenlücken in den Griff zu bekommen, wurde ein Ansatz gewählt, der die Dynamik der Ganglinien durch so genannte Features beschreibt. Die Merkmale sind so konzipiert, dass sie entweder die Grundwasserdynamik beschreiben oder eine so auffällige Eigenschaft der Zeitreihe erkennen lassen, dass entsprechende Zeitreihen zusammen gruppiert werden können.
| Feature-Name | Beschreibung |
|---|---|
| Diffsum | Variabilität, erfasst den mittleren Betrag der Steigungen, berechnet aus dem Median der Summe der Beträge aller Ableitungen |
| Ex Vals | Rauigkeit, hochfrequente Variabilität |
| Jährliche Periodizität | Stärke des Jahresgangs, berechnet durch Korrelation der mittleren jährlichen Periodizität mit der vollständigen Zeitreihe |
| Jährliche Varianz | Variabilität, Periodizität, berechnet als Median der jährlichen Varianz |
| Jumps | Inhomogenitäten, Brüche, teilweise auch Variabilität |
| Longest Recession | Unnatürlich lang abfallende Grundwasserstände, längste Sequenz ohne steigende Werte |
| Range Ratio | Überlagernde langperiodische Signale |
| Fdif | Variabilität, erfasst die Häufigkeit starker Steigungen |
| Schiefe | Inhomogenitäten, Ausreißer, häufige Extremwerte |
| Standardfehler | Streuungsmaß, standardisierte Abweichung der Zeitreihe |
| Seasonal Behaviour | Zeitpunkt des Maximums im Jahresgang |
| mup / mdown | Steig- und Fallverhalten, Symmetrie von Ganglinien-Peaks |
Grundsätzlich gibt es verschiedene Arten der Grundwasserdynamik, die mit unterschiedlichen Merkmalen unterschiedlich gut beschrieben werden können. So unterscheidet sich z. B. die typische Dynamik in einem Porengrundwasserleiter ganz erheblich von der in einem Karstgrundwasserleiter, was in der Regel andere Merkmale zur Beschreibung erfordert. Dazu werden aus den Daten selbstbeschreibende mathematische Kenngrößen extrahiert, die dann zu Gruppen zusammengefasst (geclustert) werden und im besten Fall Ganglinien gleicher Dynamik einem gemeinsamen Cluster zuordnen. Grundgedanke bei der Auswahl von Referenzmessstellen ist die Auswahl einer Messstelle, deren Dynamik repräsentativ für ein Cluster ist, d. h. die Grundwasserdynamik an den anderen Clustermessstellen im Gebiet verhält sich ähnlich wie an der Referenzmessstelle, so dass z. B. Vorhersagen von Grundwasserständen an der Referenzmessstelle auch auf den Rest des Clusters übertragbar sind.
Das Referenzmessstellenkonzept, d. h. die Reduzierung aller Messstellen auf eine überschaubare Anzahl von Referenzmessstellen, ist dem notwendigen Kompromiss zwischen technischer Machbarkeit und dem Ziel einer möglichst flächendeckenden Vorhersage geschuldet. So kann nur eine begrenzte Anzahl von Messstellen mit Datenloggern plus Datenfernübertragung ausgestattet werden und der Rechenaufwand für die monatlichen Aktualisierungen muss beherrschbar bleiben.
Bei der Definition der räumlichen Einheiten, auf die das Clustering angewendet wird, wurde die hydrogeologische Raumgliederung Deutschlands in Großräume, Räume und Teilräume gewählt (AD-HOC-AG HYDROGEOLOGIE, 2016). Ein Cluster liegt immer innerhalb eines Großraums. Bei dem gewählten Ansatz zur Clusterung von Grundwasserganglinien wird die räumliche Lage jedoch zunächst außer Acht gelassen. Das Clustering erfolgt ausschließlich auf Basis der Grundwasserdynamik der Zeitreihen, die durch die Merkmale beschrieben werden. So können sich im Idealfall Cluster bilden, die Messstellen zusammenfassen, die auch räumlich nahe beieinanderliegen und somit tatsächlich die Grundwasserdynamik eines räumlich zusammenhängenden Gebietes widerspiegeln. Es bilden sich aber auch Cluster, in denen Ganglinien zusammengefasst werden, die sich sehr ähnlich verhalten, aber räumlich nicht nah beieinanderliegen. Je nach Datenlage bilden sich auch Cluster, in denen Ganglinien gruppiert sind, die sich sehr spezifisch verhalten und keiner anderen Ganglinie ähneln. Die letztgenannten Cluster sind grundsätzlich weder für die Auswahl von Referenzmessstellen noch für eine spätere Prognose von Grundwassermessstellen geeignet und werden in der Regel verworfen. Bei den beiden anderen Clustertypen kann davon ausgegangen werden, dass sich die Messstellen bzw. Ganglinien innerhalb des Clusters ähnlich verhalten, und somit die Auswahl einer Referenzmessstelle sinnvoll ist, die später für die Vorhersage der anderen Messstellen des Clusters (unabhängig von deren räumlicher Lage) verwendet werden kann.
Das Clusterzentrum wird von der Ganglinie gebildet, deren beschreibende Features als am repräsentativsten für alle anderen Ganglinien des Clusters angesehen werden. Mit steigendem Abstand zum Clusterzentrum sinkt in der Regel auch die Ähnlichkeit zu diesem. Da das Clustern auf der Ähnlichkeit der die Ganglinien beschreibenden Features beruht, für die spätere Vorhersage aber eine Ähnlichkeit der Ganglinien hinsichtlich ihrer tatsächlichen Werte relevant ist, eignet sich der Abstand zum Clusterzentrum für die Referenzmessstellenauswahl nur bedingt. Da eine Korrelationsanalyse innerhalb der gebildeten Cluster gezeigt hat, dass die Messstellen nahe des Clusterzentrums nicht zwingend am stärksten mit allen anderen Messstellen des Clusters korrelieren, wurde für die Referenzmessstellenauswahl eines Clusters jede Ganglinie mit jeder anderen korreliert. So wurde für jede Ganglinie der Mittelwert der gewichteten Korrelations-Koeffizienten Rw berechnet und die Ganglinien nach absteigendem Rw sortiert. Als (neues) Clusterzentrum gilt damit die Messstelle, die im Schnitt am besten mit allen anderen korreliert.
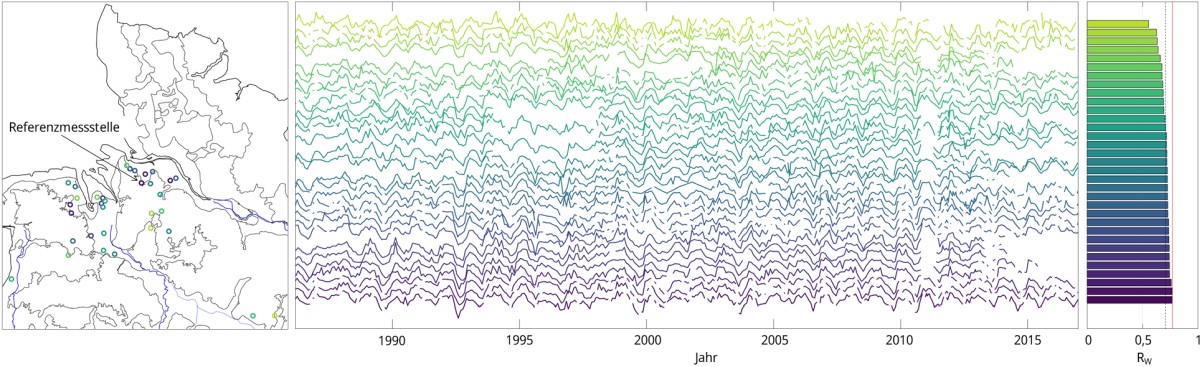
Auch bei relativ homogenen Clustern tritt der Fall auf, dass bei Ganglinien am Rande des Clusters die Korrelation zu den restlichen Ganglinien des Clusters stark abfällt. Da diese Messstellen für die Vorhersage nicht in Frage kommen, werden sie aussortiert, indem das Cluster ab einem bestimmten Schwellenwert von Rw zum Rand hin gekappt wird. Bei den meisten Clustern hat sich ein Schwellenwert von 0,5 bis 0,6 als geeignet erwiesen. Nach Kappung des Clusters wird für die verbleibenden Messstellen der Mittelwert der gewichteten Korrelations-Koeffizienten neu berechnet und die Ganglinien wiederum nach absteigendem Rw sortiert. So erhält man quasi eine bereinigte Homogenität des Clusters.
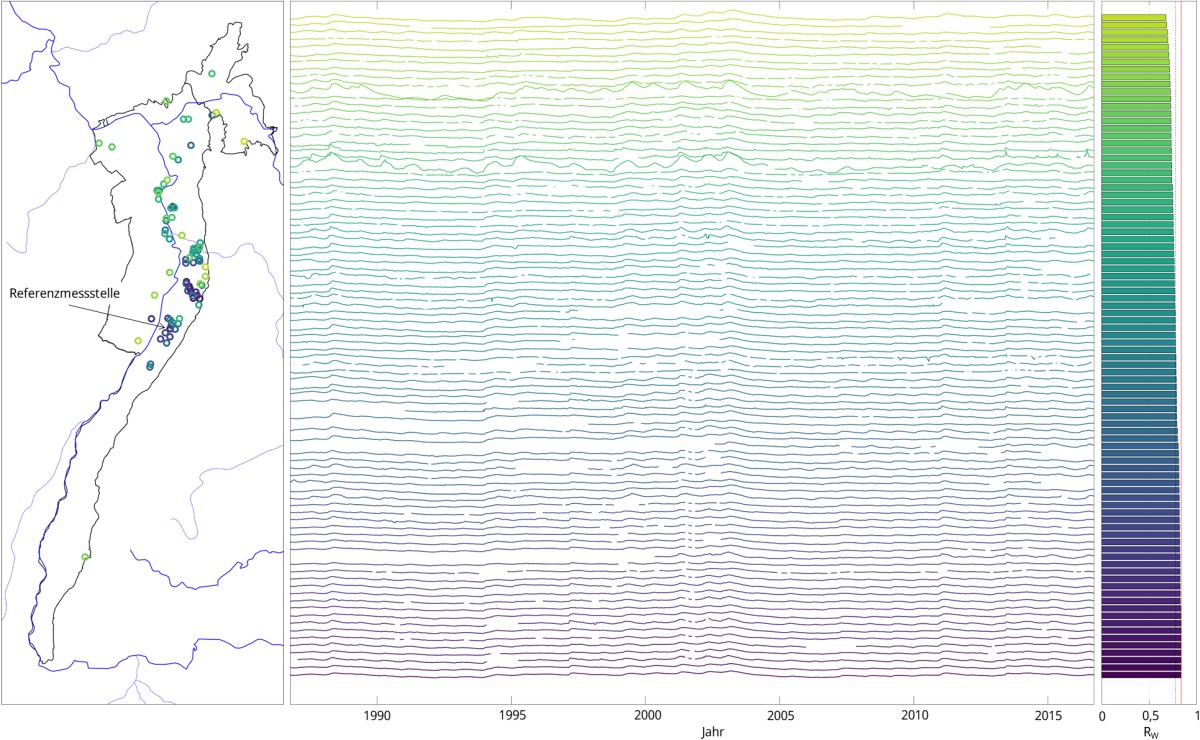
Nach der Erprobung und Optimierung des Verfahrens im hydrogeologischen Großraum 3 (Oberrheingraben mit Mainzer Becken und nordhessischem Tertiär) wurde das Verfahren auf den gesamten Datensatz übertragen. Nach Preprocessing, Eingrenzung der Untersuchungszeiträume, Aussortierung aufgrund von Inhomogenitäten sowie Überarbeitung aufgrund der Änderung des Vorhersageansatzes verblieben schließlich rund 4.200 Messstellen in rund 120 Clustern, die anhand der Referenzmessstelle des jeweiligen Clusters (Messstelle mit der höchsten Korrelation zu allen anderen Messstellen des Clusters) als potenziell geeignet für eine Kurzfristprognose eingestuft wurden.
Aufgrund der besonderen Herausforderungen von Langfristprognosen, deren Ergebnisse nicht validierbar sind, konnten nicht alle definierten Referenzmessstellen für die Mittelfristprognose sowie die Langfristprojektion verwendet werden. Stattdessen wurden auf Basis aller Referenz- und Clustermessstellen für jeden Vorhersagehorizont eigene Messstellengruppen definiert. Aus Gründen der Datenverfügbarkeit, der Modellgüte und der Plausibilität blieben für die mittelfristige dekadische Prognose 60 Grundwassermessstellen und für die Langfristprojektion bis 2100 118 Grundwassermessstellen als geeignet übrig. Die Messstellen für die Mittelfristprognose und die Langfristprojektion stimmen also nur teilweise mit denen der Kurzfristvorhersage überein.
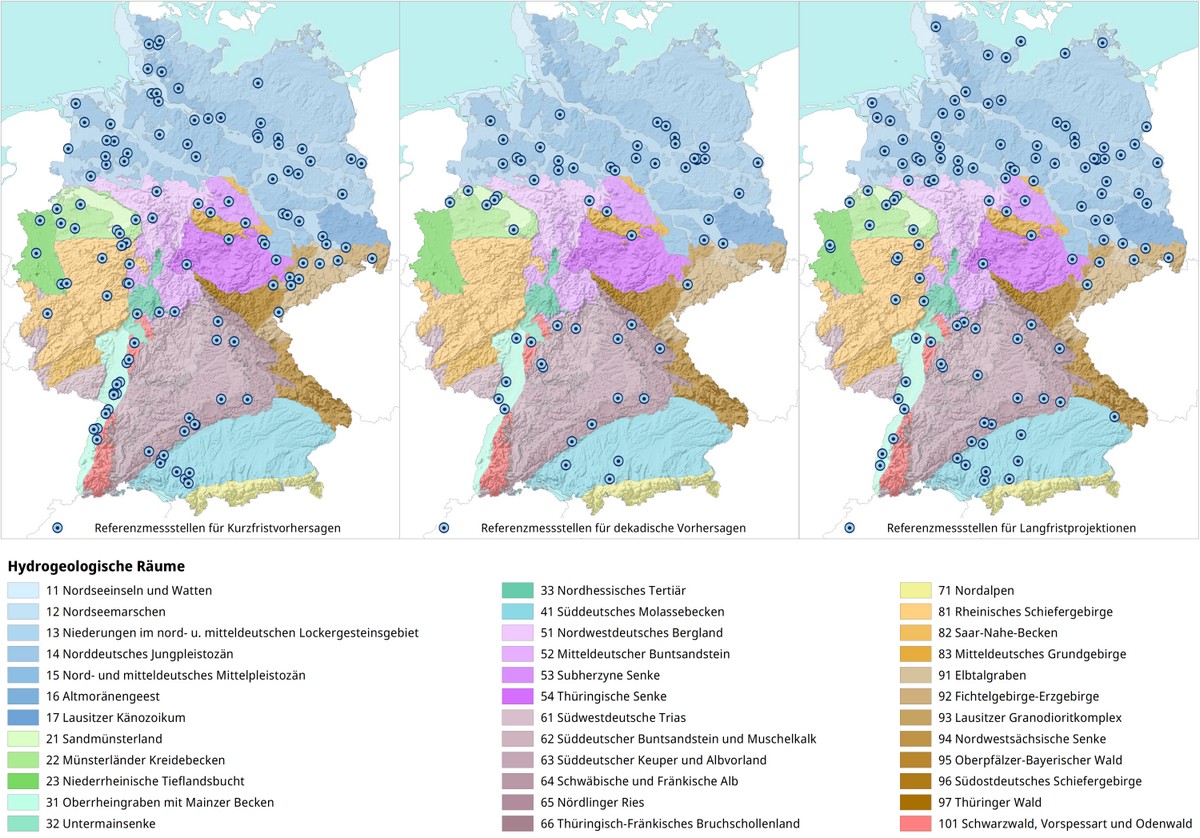
Die entwickelte Methode ist sehr gut geeignet, um die Referenzmessstellen selbst und die Messstellen, für die sie als Referenz dienen, zu definieren. Sie bietet eine Reihe von Vorteilen gegenüber den bisher verwendeten Methoden. So liefert sie ein mathematisches Gütemaß für den Zusammenhang zwischen Referenzmessstellen und Vorhersagemessstellen. Die bisher oft subjektive und von Bundesland zu Bundesland unterschiedliche Auswahl wird vereinheitlicht und mathematisch objektiviert. Darüber hinaus eröffnet sie die Möglichkeit, Zusammenhänge in den Daten zu erkennen, die bisher allein aufgrund der schieren Datenmenge nicht möglich waren.
Die Darstellung der verbleibenden Messstellen für die Kurzfristprognose zeigt teilweise eine sehr gute räumliche Abdeckung. In anderen Bereichen ist die Dichte der verbleibenden Messstellen jedoch gering, insbesondere dort, wo die Abdeckung bereits zu Beginn eher gering war. Dies dürfte in erster Linie auf die hydrogeologischen Verhältnisse zurückzuführen sein, aufgrund derer sich die Grundwasserstandsganglinien lokal sehr unterschiedlich verhalten und somit eine sinnvolle Clusterbildung erschweren (wie z. B. im Alpenvorland im Bereich des Molassebeckens), in zweiter Linie aber auch auf mangelnde Datenqualität. Insbesondere lückenhafte Daten und kurze Messzeiträume erschweren die Clusterbildung und eine anschließende Vorhersage.
Grundwasserstandsvorhersage an Referenzmessstellen:
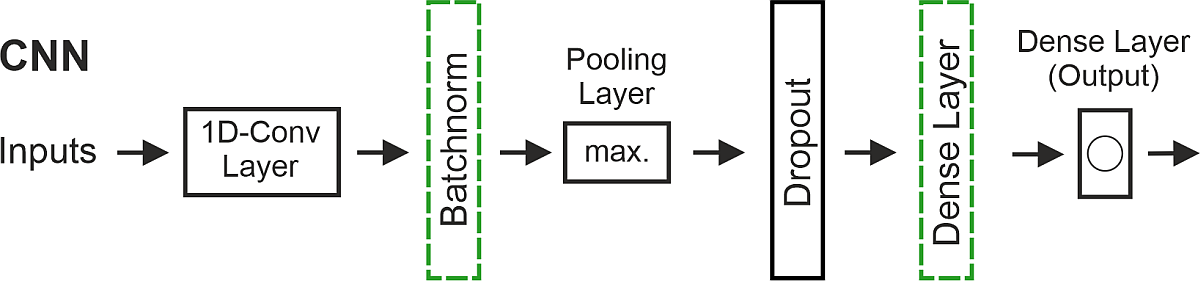
Die Anwendung von Algorithmen zur Vorhersage von Grundwasserständen basiert ebenfalls auf der Methode der künstlichen neuronalen Netze (KNN). In den letzten Jahren haben zahlreiche Studien gezeigt, dass sowohl CNN (Convolutional Neural Network)- als auch LSTM (Long Short-Term Memory)- und NARX (Nonlinear Auto-Regressive eXogenous input)-Modelle sehr gut für die Vorhersage von Grundwasserständen geeignet sind (Wunsch et al., 2021). Für die landesweite Vorhersage der Grundwasserstände werden ausschließlich eindimensionale gefaltete neuronale Netze (CNN's) verwendet.
Eindimensional gefaltete neuronale Netze (CNN's) sind eine spezielle Form von KNN's. Sie eignen sich sehr gut für maschinelles Lernen und Anwendungen der künstlichen Intelligenz (KI) im Bereich der Bild- und Spracherkennung. CNN's bestehen in der Regel aus mindestens drei verschiedenen Schichten. Convolutional Layer, der erste Typ, bestehen aus einer meist großen Anzahl von Filtern und Feature Maps. Jeder Filter hat dabei eine feste Größe, der jeweilige Input wird auch als Receptive Field bezeichnet. Schritt für Schritt werden nun alle Filter über die Eingabedaten bewegt und erzeugen so eine für jeden Filter spezifische Feature Map, d. h. jeder Filter extrahiert andere, spezifische Merkmale aus den Daten. Auf Convolutional Layer folgen in der Regel Pooling Layer, die die Feature Map des vorherigen Layers downsamplen, d. h. die Information wird konsolidiert, indem einfache Operationen wie Mittelwertbildung oder Maxima-Selektion auf Teilbereiche der Daten angewendet werden. Ähnlich wie bei LSTM-Modellen können mehrere Convolutional- und Pooling-Layer in unterschiedlicher Reihenfolge übereinandergestapelt werden. Auf die letzte Schicht folgt dann ein Dense Layer mit einem oder mehreren Ausgangsneuronen.
Als Input für das Training wurden hydrometeorologische Rasterdaten (HYRAS) des DWD verwendet, die tägliche Beobachtungsdaten mit einer Auflösung von 12,5 × 12,5 km für Niederschlag (P) und Temperatur (T) von 1951 bis 2015 enthalten. Diese liegen in verschiedenen Versionen vor, was zu unterschiedlichen Enddaten der verfügbaren Zeitreihen führt. Für die langfristigen Vorhersagemodelle wurden Niederschlag (P) v2.1 und Temperatur (T) v2.0 verwendet. Diese Daten enden zum Jahreswechsel 2015/16. Die dekadischen Prognosen beginnen im Jahr 2022, so dass neuere Klimadaten bis einschließlich 2021 benötigt wurden. Daher wurde zum einen auf die neueren Versionen Niederschlag v3.0, sowie Temperatur v4.0 und relative Feuchte (rH) v4.0 zurückgegriffen. Niederschlag v3.0 wird laufend aktualisiert und online zur Verfügung gestellt, Temperatur endet jedoch wie die Vorgängerversionen derzeit noch im Jahr 2015. Die entstandene Lücke bis 2022 wurde mit Daten aus E-OBS v25.0e (Copernicus Klimawandeldienst C3s) geschlossen. Dabei handelt es sich um einen europäischen Datensatz gerasterter und regionalisierter Klimabeobachtungsdaten. Sobald verfügbar, werden die E-OBS-Daten durch HYRAS-Daten ersetzt.
Zur Bewertung der Vorhersagegüte von Grundwasserständen wurden Hindcasts des DWD verwendet, da für den operativen Betrieb keine Beobachtungsdaten verfügbar sind. Hindcasts, auch Nachhersagen oder Rückwärtsprognosen genannt, sind Vorhersagen, die in der Vergangenheit gestartet und mit Beobachtungen verglichen werden, um die Qualität der Vorhersagen zu bewerten. Für die Erstellung des Rasterdatensatzes wurde das empirisch-statistische Downscaling-Verfahren EPISODES. genutzt, welches vom DWD entwickelt wurde. Das Verfahren basiert auf saisonalen Vorhersagen des Deutschen Klimavorhersage-Systems (German Climate Forecast System – GCFS). Für die Jahre 1990 bis 2017 stehen modellbasierte Rückberechnungen von Tagesdaten für Niederschlag und Temperatur mit einer Auflösung von 12,5 × 12,5 km zur Verfügung.
| Kurzfristvorhersagen (1 Woche, 1 Monat, 3 Monate) | Dekadische Prognosen (2022 - 2031) | Langfristprojektionen (bis 2100) |
|
|---|---|---|---|
| Training | DWD-HYRAS- und Copernicus E-OBS-Daten | bis 2015: DWD-HYRAS-Daten ab 2016: DWD-HYRAS- & Copernicus E-OBS-Daten | DWD-HYRAS-Daten |
| Evaluierung | DWD-HYRAS- und Copernicus E-OBS- / ERA5-Land-Daten sowie EPISODES-Hindcasts des DWD | DWD-HYRAS- und Copernicus E-OBS-Daten | DWD-HYRAS-Daten |
| Operationelle Vorhersage | EPISODES-Daten des DWD | Ensembledaten des MPI-ESM-LR | DWD-Kernensemble RCP-Szenarien 2.6, 4.5 und 8.5 |
Als Grundlage für die dekadischen Vorhersagen wurden Daten des Erdsystemmodells des Max-Planck-Instituts für Meteorologie in niedriger Auflösung (MPI-ESM-LR) verwendet. Diese wurden mithilfe der EPISODES-Methode bearbeitet und in einer geographischen Auflösung von 5 km und bias-adjustiert auf Beobachtungsdaten zur Verfügung gestellt. Des Weiteren stehen die Daten als Ensemblesimulationen in 16 verschiedenen Modellläufen zur Verfügung. Die Simulation beginnt im Jahr 2021 und der Vorhersagezeitraum umfasst die Jahre 2022 bis 2031.
Im Fall der Langfristprojektionen wurden die Modelle des DWD-Kern-Ensembles genutzt, um Inputdaten zu generieren. Es wurde eine Untersuchung der drei RCP-Szenarien 2.6, 4.5 und 8.5 durchgeführt, die repräsentative Konzentrationspfade gemäß dem Weltklimarat zur Beschreibung von Szenarien für den Verlauf der absoluten Treibhausgaskonzentration in der Atmosphäre darstellen. Die Auswertung erfolgte mittels einer linearen Trendanalyse der Jahresmittelwerte und der Analyse der Veränderungen zwischen dem Start im Jahr 2014 und dem Ende der Simulation im Jahr 2100 (Wunsch et al., 2022).
Literatur:
AD-HOC-AG HYDROGEOLOGIE (2016): Regionale Hydrogeologie von Deutschland - Die Grundwasserleiter: Verbreitung, Gesteine, Lagerungsverhältnisse,
Schutz und Bedeutung. - Geol. Jb., A 163: 456 S., 264 Abb.; Hannover.
KREIENKAMP, F., PAXIAN, A., FRÜH, B. et al. (2019): Evaluation of the empirical–statistical downscaling method EPISODES. - Clim Dyn 52, 991–1026. doi: 10.1007/s00382-018-4276-2.
WUNSCH, A. & LIESCH, T. (2022): Anwendung neuer Vorhersageprodukte. - Zwischenbericht Arbeitspaket 3, 39 S., 22 Abb., 4 Tab.; KIT, Karlsruhe.
WUNSCH, A. & LIESCH, T. (2021): Entwicklung, Anwendung und Evaluierung von Deep Learning Ansätzen zur Grundwasserstandsvorhersage.
- Zwischenbericht Arbeitspaket 1, 83 S., 24 Abb., 1 Tab., 4 Anh.; KIT, Karlsruhe.
WUNSCH, A. & LIESCH, T. (2020): Entwicklung und Anwendung von Algorithmen zur Berechnung von Grundwasserständen an Referenzmessstellen auf Basis der Methode Künstlicher Neuronaler Netze. - Abschlussbericht Projektphase I, 183 S., 61 Abb., 11 Tab., 13 Anh.; KIT, Karlsruhe. doi: 10.5445/IR/1000136522.
WUNSCH, A., LIESCH, T., BRODA, S. (2022): Deep learning shows declining groundwater levels in Germany until 2100 due to climate change. - Nat
Commun 13(1), 1221. doi: 10.1038/s41467-022-28770-2.
WUNSCH, A., LIESCH, T. & BRODA, S. (2022): Feature-based Groundwater Hydrograph Clustering Using Unsupervised Self-Organizing Map-Ensembles. - Water Resour. Manage., 36(1): 39-54. doi: 10.1007/sll269-021-03006-y.
WUNSCH, A., LIESCH, T., BRODA, S. (2021): Groundwater level forecasting with artificial neural networks: A comparison of long shortterm memory
(LSTM), convolutional neural networks (CNNs), and non-linear autoregressive networks with exogenous input (NARX). - Hydrol. Earth Syst.
Sci. 25 (3), pp. 1671-1687. doi: 10.5194/hess-25-1671-2021.